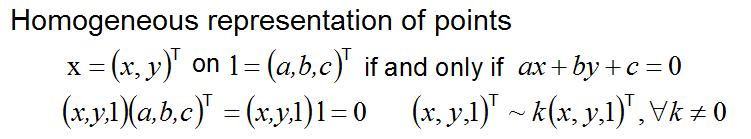이전 포스트에서 나왔던 평면에 대한 성질을 다시 정리해보자면 아래와 같다.
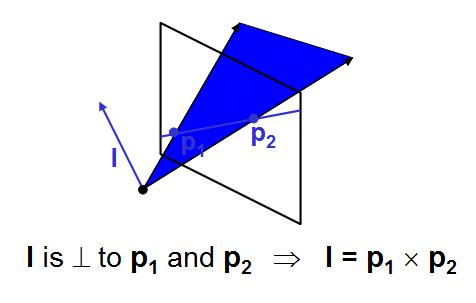
(1) 위는 두개의 점(벡터)를 cross 곱을 해서 나오는 직선 l 은 두 점을 가로지른다는 의미이다. 그 방향은 두점이 만들어내는 평면에 수직한 방향이 되겠다.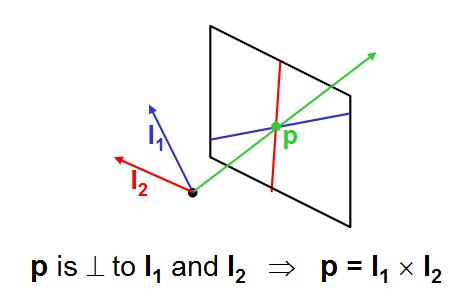 (2) 두 직선에 대해 cross 곱을 하게 되면 나타나는 점은 두 직선의 교점이 되는데, 이 역시 방향은 두 직선이 만들어내는 평면에 수직한 방향이 된다.
(2) 두 직선에 대해 cross 곱을 하게 되면 나타나는 점은 두 직선의 교점이 되는데, 이 역시 방향은 두 직선이 만들어내는 평면에 수직한 방향이 된다.
이렇게 해서 단지 수식에 대해서만 나타내면 상상하기 어려운 것이 도식화 되었다.
그럼 이제 Ideal points 와 line 을 알아보자.
평행한 직선의 교점
평행한 직선에 교점이 있을리 없지만, 일단 알아보자.
두 직선 ax+by+c=0과 ax+by+c'=0 에 대해 위의 결과 (2) 를 생각해 보자.
각 직선을 l, l' 라고 하면 l x l' 는 (c'-c)(b,-a,0)T로 나타난다.
풀어서 계산하면 아래와 같다.
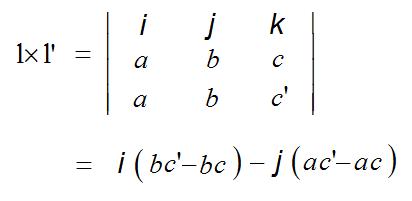 i, j, k 가 x, y, z 축의 단위벡터이므로 이를 통해 계산하고 같은 항을 빼내면,
i, j, k 가 x, y, z 축의 단위벡터이므로 이를 통해 계산하고 같은 항을 빼내면,
(c'-c)(b,-a,0)T 가 된다.
(c'-c)은 단지 상수가 되고, (b,-a,0)T 이 점이다. 여기서 inhomogeneous 표현을 가져오면 (b/0,-a/0)T 이 되는데, 0이 분모에 있으므로 무한히 큰 좌표라고 제안하자.
일반적으로 homogemeous 좌표계에서 점 (x, y, 0)T 는 유한한 평면 R2에서 어떤 점과 일치하지 않는다. 이것은 무한한 곳에서 평생선은 만난다는 것을 내포하고 있다.
음...

(1) 위는 두개의 점(벡터)를 cross 곱을 해서 나오는 직선 l 은 두 점을 가로지른다는 의미이다. 그 방향은 두점이 만들어내는 평면에 수직한 방향이 되겠다.
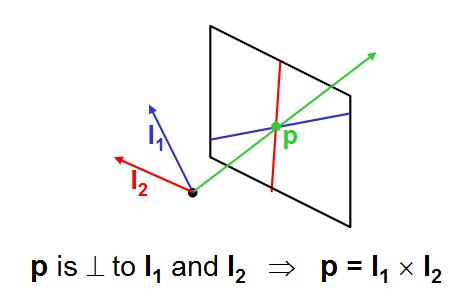
이렇게 해서 단지 수식에 대해서만 나타내면 상상하기 어려운 것이 도식화 되었다.
그럼 이제 Ideal points 와 line 을 알아보자.
평행한 직선의 교점
평행한 직선에 교점이 있을리 없지만, 일단 알아보자.
두 직선 ax+by+c=0과 ax+by+c'=0 에 대해 위의 결과 (2) 를 생각해 보자.
각 직선을 l, l' 라고 하면 l x l' 는 (c'-c)(b,-a,0)T로 나타난다.
풀어서 계산하면 아래와 같다.
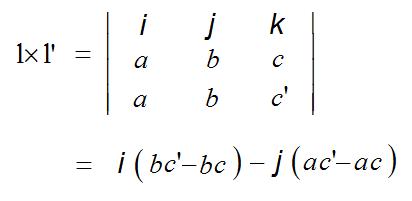
(c'-c)(b,-a,0)T 가 된다.
(c'-c)은 단지 상수가 되고, (b,-a,0)T 이 점이다. 여기서 inhomogeneous 표현을 가져오면 (b/0,-a/0)T 이 되는데, 0이 분모에 있으므로 무한히 큰 좌표라고 제안하자.
일반적으로 homogemeous 좌표계에서 점 (x, y, 0)T 는 유한한 평면 R2에서 어떤 점과 일치하지 않는다. 이것은 무한한 곳에서 평생선은 만난다는 것을 내포하고 있다.
음...