3D Vision - 2D Projective Geometry
3차원 비전 컴퓨팅을 위해 "Multiple View Geometry in computer vision"의 내용을 정리하고 고찰해 보고자 한다. (책은 구글북스에서 볼 수 있는데, 제목을 클릭하면 이동함)
이 책의 내용에서 1장에서는 전반적인 책의 흐름과 각 방법들의 개략적인 전개를 보여주는데, 여기에서 너무많은 시간을 보내지 않았으면 한다. 왜냐하면 별안간 등장하는 유클리드 기하학과 변환행렬들의 구조를 알아내려고 하면 초반에 너무많은 시간을 허비하게 되기 때문이다. 사실상 뒤의 장에서 다 소개하고 있으므로, 바로 2장부터 알아보겠다.
<2D Projective Geometry>
* 기본정의
점과 선은 행렬과 벡터로 표현하게 된다. 통상적으로 두 행렬과 벡터의 곱으로 표현하게 되는데, 행렬은 오른쪽의 열이고 벡터는 왼쪽의 행이 된다.
행 (행렬) X 열 (벡터)
* 점과 선
통상 평면위의 직선은 ax+by+c=0 으로 표현된다. 즉 다르게 표현하면 (x,y,1)(a,b,c)T=0 이 된다. 0이 아닌 상수를 곱하게 되면 (ka)x+(kb)y+(kc)=0 이 된다.
벡터 (a,b,c)T 는 k(a,b,c)T 로 나타낼 수 있고 같은 선에 있다. 직선방정식을 볼때, 모든 항에 상수를 곱해도 동일한 직선이 되므로 공감이 갈 것이다.
* Homogeneous 표현
직선 l=(a,b,c)T 위의 점을 x =(x,y)T 로 나타내자. 이때 직선방정식은 ax+by+c=0 이라고 할때에 (x,y,1)(a,b,c)T = (x,y,1)l = 0 으로 표시할 수 있다.
homogeneous 벡터의 표현으로 점을 표시하면 x = (x1,x2,x3)T 가 되는데 R2 평면에 대한 표현은 (x1/x3, x2/x3)T 가 된다.
homogeneous 좌표에 대해서는 추후에 다시 논의 하겠지만, 우리가 느끼는 3차원 공간과 헷갈리지 않도록 유의해야 한다.

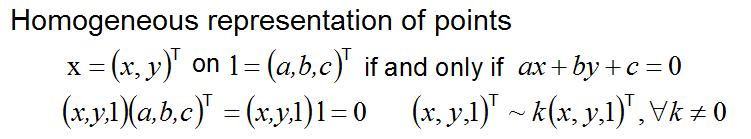
The point x lies on the line l if and only if xTl=lTx=0

* 자유도
직선방정식에서 x와 y 두가지 좌표값이 명확하게 제공되어야 한다. 즉 직선에 대한 두 매개변수에 의해 형태가 결정되므로 자유도는 2라고 한다.

